Introduzione

Sono un ingegnere elettrico (quando mi sono laureato si diceva “elettrotecnico”, termine ormai antiquato) e faccio uso quotidiano dei fogli di calcolo, che sono utilissimi nel mio lavoro nel campo dell’energia e dell’idraulica. 

Come tanti altri prima di me, già nel primo anno di pandemia ho iniziato a pormi molti dubbi sui dati e sulla narrazione che venivano diffusi H24 dalle Istituzioni e dai principali organi d’informazione.

Col passare del tempo, le perplessità sulle decisioni della Scienza e di chi diceva di parlare in Suo nome non hanno fatto che aumentare: sembravano mirate a impedire di curare gli ammalati, intasare i pronto soccorso e ostacolare la ricerca delle cause specifiche di morte.

L‘arrivo tanto atteso dei “vaccini”, se da un lato mi ha fatto scoprire di essere un “no vax” per aver rifiutato un non-vaccino, dall’altro ha stravolto i principi della medicina permettendo di iniziare le somministrazioni di un farmaco (sperimentale) a meno di un anno dalla scoperta dei primi casi di un’infezione definita “sconosciuta”. 

Quando si è iniziato a sentire con sempre maggiore insistenza di bambini e adolescenti morti d’infarto o di “malore improvviso” mentre gli Istituti di vigilanza sanitaria negavano fermamente qualsiasi aumento di mortalità giovanile, è stato il punto di svolta. Ho deciso di spendere ore e ore della mia vita, molte delle quali di notte, e mettere a frutto la mia familiarità coi fogli di calcolo per elaborare i dati ufficiali e costruirmi da solo le informazioni che non trovavo da nessuna parte. Con l’intento ovviamente di divulgarle, se avessi trovato qualcosa di interessante.

Dopo un periodo di purgatorio passato a cercare di decifrare gli immensi file di raccolta dei decessi resi disponibili da Istat (per la cui estrazione usufruisco tuttora dell’appoggio dell’ing. Trambusti, che nel frattempo ho conosciuto e con cui si è sviluppata una collaborazione e una sincera amicizia), mi è stato possibile costruire una struttura di calcolo per elaborare in maniera sistematica l’eccesso di mortalità della popolazione suddivisa per classi d’età e per genere.  In aggiunta, ho scelto di visualizzare congiuntamente in appositi grafici gli andamenti temporali dell’eccesso di mortalità e delle somministrazioni vaccinali. Non sapevo a priori cos’avrei trovato: l’intento era ricostruire realtà complesse a partire dai dati più elementari, senza nessun filtro posto da elaborazioni esterne.  Volevo vederci chiaro.

Questa struttura di calcolo è stata oggetto di continui perfezionamenti, ma fin dall’inizio mi ha rivelato uno scenario che più che interessante definirei inquietante.

Il che mi ha fornito la motivazione per continuare ad ampliare la ricerca fino a renderla meritevole della massima divulgazione.  Credo che adesso il momento sia arrivato.

Ho svolto la medesima ricerca coi dati nazionali, e coi dati di tutte le regioni e province autonome, arrivando a mettere insieme un volume notevole di documentazione che è consultabile a questo link (….). Nei prossimi capitoli cercherò di descrivere le parti salienti di questo studio.

Per valutare autonomamente l’eccesso di mortalità ho dovuto studiare, a partire dalla definizione più generale che se ne dà, ai metodi di calcolo più utilizzati dagli Istituti di statistica e di sorveglianza sanitaria e dalle Istituzioni in generale. Ho visto che non esiste un metodo univoco, che metodi diversi danno risultati diversi, e ho dovuto fare delle scelte.  Ho scelto appositamente come base il metodo più semplice e più cautelativo, ma più largamente utilizzato dalle Istituzioni: in tal modo i miei risultati sono direttamente confrontabili. Ho poi introdotto una variante più raffinata, anch’essa molto utilizzata. Gli amici matematici a volte storcono il naso per la semplicità dei miei algoritmi di calcolo, ma io difendo i miei metodi per due motivi: in primis per la diretta confrontabilità dei risultati con quelli ufficiali; inoltre, più che dati meramente numerici mi interessavano le variazioni.

Una volta messo a punto il mio strumento, ho potuto constatare che le Istituzioni omettono di segnalare le realtà scomode, arrivando anche a negarle spudoratamente. Ho imparato molto presto anche i trucchetti che vengono messi in atto per farlo, che sono in realtà molto goffi e ripetitivi.

Il secondo passo è stato mettere a confronto, in maniera sistematica, l’andamento dell’eccesso di mortalità con quello delle somministrazioni vaccinali. Non sono partito con un risultato prefissato, né tantomeno pensavo di poter arrivare a dimostrare nessi causali, ma avevo la possibilità di monitorare capillarmente su un periodo di quattro anni l’andamento della mortalità in corrispondenza della più grande campagna di somministrazione pressoché universale di un farmaco (sperimentale).

Da subito i risultati mi hanno fatto suonare un campanello d’allarme.

Tra le popolazioni giovanili, i casi di eccesso di mortalità (quelli negati dalle Istituzioni e dalla narrazione dominante) erano sempre di poco preceduti da periodi di intensa somministrazione, e spesso a livello grafico ne copiavano addirittura la forma!

Ho potuto verificare che determinati gruppi di popolazione erano più colpiti di altri da anomalie nella mortalità, e le dinamiche si ripetevano molto simili in diverse regioni.

Si può obiettare che un confronto di tipo grafico può trarre in inganno e la variazione sincrona di due curve può essere un fatto casuale che non comporta nessuna reciproca influenza tra le due.

Il problema è nel numero di volte che un evento può ripetersi per continuare a definirlo casuale: la definizione regge se il numero raggiunge le due o tre cifre?   Scorrendo i numerosi grafici nazionali e regionali disponibili, risulta evidente la frequenza con cui ai periodi di somministrazioni corrispondono repentini peggioramenti nell’andamento della mortalità.  Ciò si riscontra ovunque ma è più ricorrente nelle regioni del Sud.

Per le popolazioni più anziane le dinamiche sono diverse, ma salta all’occhio che la mortalità in generale non accenna mai a diminuire, continuando a crescere anche dopo i due picchi pandemici e l’inizio delle vaccinazioni, mentre nelle regioni del Centro e del Sud inizia in concomitanza con le vaccinazioni.

In conclusione: metto a disposizione il mio lavoro non per dare delle risposte, ma per porre delle domande che chi ha in carico la salute pubblica non potrà continuare a eludere all’infinito.

L’eccesso di mortalità, e i trucchetti per farlo sparire

Il primo punto da chiarire è che per tutta la trattazione mi riferisco alla mortalità generale, vale a dire senza distinzione di causa. Selezionare una causa specifica (es. Covid-19) implicherebbe introdurre criteri di selezione e quindi arbitrarietà. L’eccesso di mortalità è oggetto di analisi per gli anni che vanno dal 2020 al 2023.

Ciò premesso: qual è la definizione di “eccesso di mortalità”, e come si calcola?

La definizione più generale è: differenza tra i decessi accertati in un certo periodo e i decessi attesi nello stesso periodo.  È ovvio che questa differenza può anche essere negativa, anche se il termine “eccesso” può far pensare il contrario.

È altrettanto ovvio che il problema si sposta sulla valutazione dei decessi attesi, e qui si apre un mondo.  Per valutare i decessi attesi occorre fare due scelte: il periodo di riferimento, e il modello con cui elaborare i dati disponibili in tale periodo.

Per la scelta del periodo di riferimento, si trovano diverse scelte in letteratura.

Istat in genere prende a riferimento il “quinquennio pre-pandemico”, vale a dire gli anni 2015–2019 (1), anche se per alcune analisi ha considerato il biennio 2018-2019 (2). 

Anche il prestigioso sito di statistica “Our World in Data” fa riferimento al quinquennio 2015-2019 (3). 

Eurostat fa riferimento al quadriennio 2016-2019 (4).

L’OMS, o WHO in inglese, in genere considera il quinquennio 2015-2019 (5).

È possibile riferirsi anche a periodi più lunghi, generalmente non oltre l’intervallo 2011-2019.

Supponendo di aver scelto il periodo, veniamo al metodo di elaborazione dei dati. Il più semplice in assoluto è fare la media dei decessi nel periodo di riferimento. I valori medi così trovati si dovranno poi rapportare alle variazioni demografiche (quest’ultimo punto sarà ampiamente ripreso nel seguito). Questo metodo, il più semplice, presenta il limite di non tener conto della tendenza temporale dei decessi: in presenza di un andamento in aumento o diminuzione è lecito attendersi negli anni successivi valori che seguano la stessa tendenza.  Si possono quindi realizzare estrapolazioni della tendenza, mediante regressioni lineari (individuando la retta che meglio interpreta l’andamento pregresso) o mediante funzioni matematiche di complessità crescente.

Un esempio di valutazione dei decessi attesi, o baseline mediante regressione lineare è quello utilizzato dal sito Our World in Data (3).

Metodi molto sofisticati possono talvolta portare a brutte sorprese come testimonia l’incidente occorso alla stessa WHO nel 2022 nel valutare l’eccesso di mortalità in Germania, episodio in seguito battezzato “German puzzle” (6).  Analogamente, un eccessivo uso di regressione lineare per le classi giovanili può portare a sovrastime come testimoniato dal “disclaimer” di Euromomo nel 2023 (*)

https://www.euromomo.eu/bulletins/2023-16

I metodi di valutazione dei decessi attesi, e quindi dell’eccesso di mortalità come si è visto non sono univoci. Ovvio che metodi diversi possono avere pro e contro e possono dare risultati diversi, più o meno cautelativi e più o meno affidabili.  L’importante è che il metodo usato sia chiaro ed applicato rigorosamente, per dare la possibilità al lettore di interpretare correttamente i risultati e per descrivere adeguatamente le tendenze, che non sono meno importanti dei valori assoluti.

Metodi scelti per questo studio

Fatte le dovute premesse, forse un po’ noiose, passiamo alle basi utilizzate per lo studio in oggetto.

Il periodo di riferimento prescelto è il quinquennio 2015-2019, poiché è quello che più comunemente si ritrova nelle pubblicazioni e nei dibattiti più o meno scientifici. Per quanto riguarda i metodi di elaborazione dei dati, si sono utilizzate sia la media del periodo che la regressione lineare (entrambe ponderate sulle variazioni demografiche).

La valutazione dei decessi attesi tramite la media, che utilizzo preferibilmente per le classi giovanili (< 50 anni) fornisce dati cautelativi, nel senso che in genere sottostima leggermente l’eccesso di mortalità rispetto a metodi più sofisticati.

Ciò poiché in generale i tassi di mortalità, perlomeno a partire dal 2011, oscillano intorno a una linea in discesa. Utilizzo comunque questo metodo intanto perché è comunemente usato anche dagli istituti di statistica; inoltre per alcune classi giovanili nel quinquennio in esame l’andamento dei tassi di mortalità è tutt’altro che regolare, e un’estrapolazione potrebbe portare forti distorsioni (*). Cionondimeno, per alcune classi d’età giovanili con dati più regolari vale la pena di utilizzare entrambi i metodi. Per le classi d’età più anziane (> 50 anni) è sicuramente preferibile l’analisi con la regressione lineare.

Con la regressione lineare, stimo i valori che si sarebbero avuti nel 2020 se si fosse mantenuta la tendenza dei cinque anni precedenti, e mantengo questo valore come riferimento da lì in poi.  In questo modo, il numero di decessi attesi preso a riferimento è lo stesso per l’anno pandemico e per gli anni a seguire.

Un grafico aiuta a capire meglio la differenza tra i due metodi.

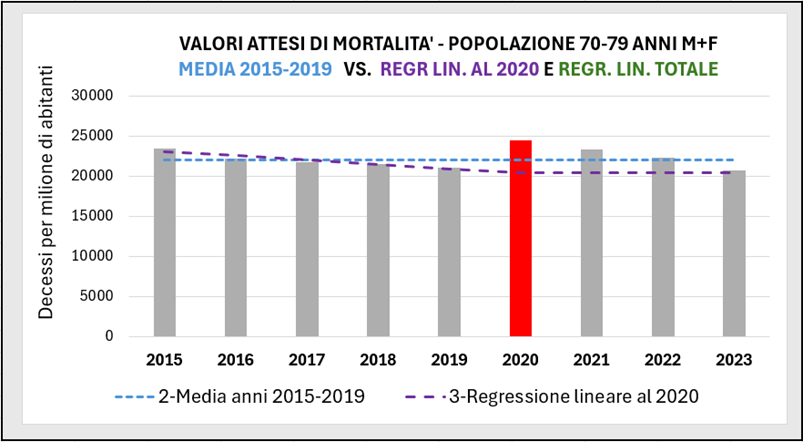
Figura …

Dalla figura sopra si capisce agevolmente che considerare il valor medio dei 5 anni pre-pandemici non terrebbe conto dell’andamento dei tassi di mortalità e darebbe valori attesi maggiori. In questo caso abbiamo a che fare con una popolazione anziana con andamento regolare (in discesa) dei tassi di mortalità.

È evidente che la scelta dei valori attesi mediante regressione lineare comporterà valori maggiori di eccesso di mortalità, e certamente più corretti.

In ogni caso, il valore dato dalla media dei decessi sul quinquennio, puro o corretto secondo la regressione lineare, dev’essere riportato al numero di abitanti di cui si compone la popolazione in esame per ogni anno oggetto di valutazione, mediante una semplice proporzione col numero medio di abitanti durante il periodo di riferimento.

 Il motivo per cui occorre rapportare i decessi medi al variare della demografia è piuttosto evidente: se ad esempio il numero di residenti fosse diminuito del 10% tra il periodo di riferimento nel quale si contano i decessi e se ne fa la media, e l’anno per il quale si calcola l’eccesso, è ovvio che a parità di condizioni anche il numero dei decessi dovrebbe diminuire del 10%

Si veda sotto il grafico che mostra il numero di residenti in Italia (al primo gennaio) negli anni dal 2015 al 2023, per ognuna delle classi d’età considerate. È palese che nelle classi d’età giovanili (fino a 49 anni) tendono a scendere (fa eccezione la classe 10-19 anni), mentre dai 50 anni in su tendono a salire.

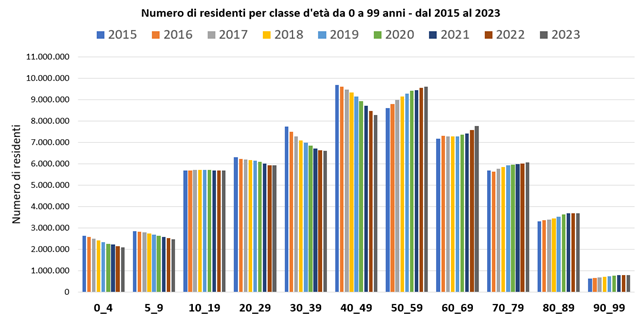
Figura …..

Nella successiva figura si può apprezzare la diminuzione anche quantitativamente: ponendo a 1 il valore medio 2015-2019 del numero di residenti di ognuna delle classi d’età giovanili, per alcune classi d’età il valore nel 2023 (al 1° gennaio) è nettamente inferiore a 0,9.

Ricapitolando:

L’analisi dell’eccesso di mortalità fa riferimento ai decessi per tutte le cause, interessa il periodo dal 1° gennaio 2020 al 31 dicembre 2023, usa come riferimento sia la media dei decessi dal 2015 al 2019 che la regressione lineare degli stessi proiettata al 2020, e in ogni caso tiene conto delle variazioni demografiche.

Vediamo ora su quali gruppi di popolazione si sono applicati questi metodi di calcolo.

Per lavorare su gruppi di popolazione sufficientemente omogenei nel numero di decessi e nella causa degli stessi, ho suddiviso la popolazione totale di ogni area geografica trattata (ad es. l’Italia, o una Regione) in 12 classi d’età. A loro volta questi gruppi sono suddivisi in tre secondo il genere: totale,

Figura

maschile e femminile. Quindi in tutto, per ogni area geografica in esame, questa analisi si ripete 36 volte.

Le classi d’età sono decennali (10-19, 20-29, ecc.), tranne le prime due quinquennali (0-4 e 5-9) e l’ultima che è una classe aperta (100+).

Questa griglia piuttosto fitta garantisce che eventuali anomalie nei decessi di uno specifico gruppo di popolazione non vengano nascoste accorpando serie di dati con numeri piccoli con altre dai numeri molto più grandi e magari in controtendenza.

Vorrei ora mostrare com’è facile, omettendo (per colpa o per dolo) questo tipo di precauzioni, giungere a conclusioni fuorvianti come spesso accade agli showmen televisivi e purtroppo anche alle Istituzioni.

Come dissimulare ad arte gli eccessi di mortalità

Le tecniche deliberate (o errori pacchiani, il risultato non cambia) che portano a strafalcioni sono essenzialmente tre:

• Confrontare numeri assoluti di decessi, e non tassi di mortalità, tra anni differenti
• Aggregare gruppi di popolazione fortemente disomogenei, o intervalli di età eccessivi
• Non separare le popolazioni per genere.

Tra gli esempi pratici di disinformazione, una menzione di rilievo spetta alla trattazione dell’eccesso di mortalità “under 50” negli anni 2021-2022 da parte di autorevoli Istituti di vigilanza sanitaria e statistica tra cui I.S.S. e Istat, in un documento datato luglio 2023 (7).

In questo documento viene più volte negata l’esistenza di eccesso di mortalità under 50 “rispetto alla baseline della media 2015-2019” (cosa che come vedremo non corrisponde a verità), e tra gli argomenti a “dimostrazione” di questo assunto viene proposto un grafico multiplo (Fig. ..) che definirei imbarazzante …  Questa (brutta) figura pone nello stesso grafico piuttosto affollato il numero di decessi attesi e registrati (in numeri assoluti) nel 2021 e 2022 per tutta la popolazione da 0 a 50 anni. 

  Figura ..   originariamente Figura 5/A del documento di I.S.S., Istat ecc. (7)

Questi esperti sono riusciti in un colpo solo a mettere in atto tutte e tre le tecniche di dissimulazione elencate sopra.  In un grafico del genere, un eccesso di mortalità del 50% a carico degli adolescenti, di per sé tragedia immane, si confonderebbe con lo spessore della linea.  Chapeau!

Un altro esempio di “gioco delle tre carte” coi dati di mortalità è quello proposto con l’abituale eleganza da un notissimo tele-virologo, ospite fisso dei salotti televisivi.

In un grafico pubblicato sul suo profilo Facebook nell’aprile del 2024 (Fig. ..), questo Uomo di Scienza denuncia l’infondatezza degli allarmi dei soliti complottisti, mostrando che le variazioni percentuali dei tassi di mortalità del 2023 di vari gruppi di popolazione, compresi quelli giovanili, sono tutte in negativo rispetto ai rispettivi valori medi del 2015-2019.

Peraltro, se si vanno a verificare questi dati uno per uno, sono corretti.

Il problema è che non permettono di trarre le conclusioni sostenute dal tele-virologo.

Vediamo perché.

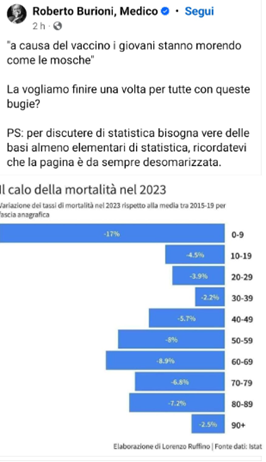
Figura .. – Post Facebook di Roberto Burioni (aprile 2024)

Intanto dobbiamo riconoscere che questo tentativo è più sofisticato del precedente, in quanto perlomeno parla di tassi di mortalità e non di numeri assoluti e quindi la prima tecnica di dissimulazione non viene usata. Ma le altre due si, e qui casca l’asino.

Prendiamo la prima classe d’età: da 0 a 9 anni. Ebbene, basta vedere i dati di mortalità di qualunque anno per rendersi conto che il numero di decessi del gruppo 0-4 anni è circa 9 (nove) volte maggiore di quello dei bambini da 5 a 9 anni, perché comprende tutti i decessi neonatali.  Pertanto, se si vuole nascondere quello che accade ai bambini in età scolastica, il modo migliore è quello di accorparli alla prima fascia.

Nella seconda classe d’età, quella degli adolescenti, il dato scomodo è nascosto dall’ accorpamento di genere. Si deve sapere che nelle età giovanili, il numero di decessi maschili equivale a oltre il doppio di quelli femminili: si tratta prevalentemente di decessi di tipo traumatico ed entra in gioco la maggior turbolenza dei maschi, più soggetti ad incidenti stradali, o ai suicidi (nei maschi quattro volte più frequenti che nelle femmine).  Anche in questo caso, quindi, per nascondere anomalie nella mortalità delle ragazze il modo migliore è mostrare i dati insieme a quelli dei ragazzi.

Andando a correggere queste “sviste”, si ottiene uno scenario decisamente diverso.

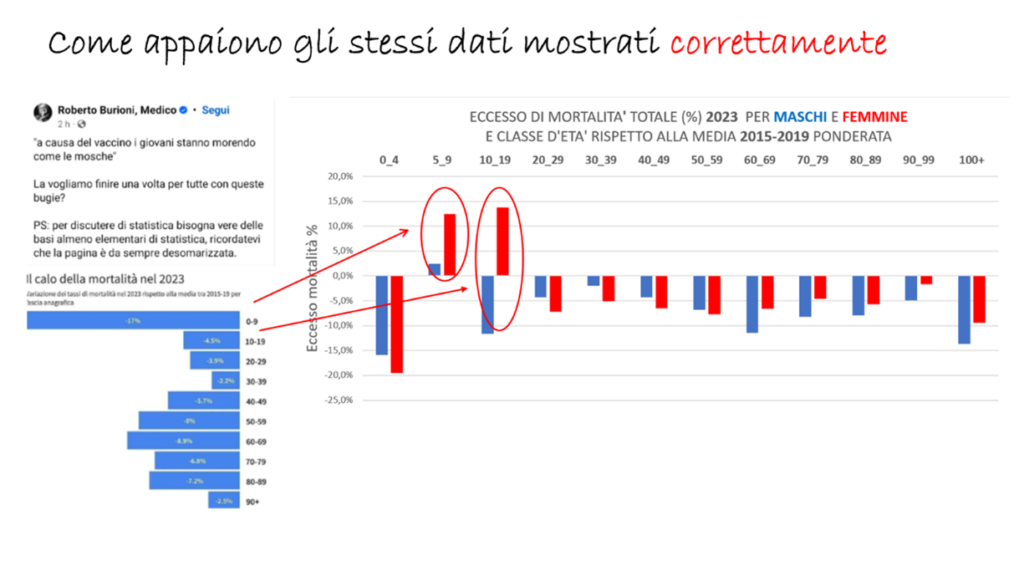
Figura …. Dati di mortalità di cui alla Fig. precedente, mostrati più correttamente

Come si vede nella Fig. .. , mostrati correttamente i dati rivelano gravi anomalie proprio a danno dei giovanissimi e in particolare nel genere femminile. Da notare che i dati dei decessi dei gruppi a cui erano accorpati (oltre ad essere basati su numeri maggiori), guarda caso erano in controtendenza. 

In realtà anche i bambini maschi denunciano un lieve eccesso peraltro iniziato nel 2022, e gli adolescenti un deciso peggioramento nei tassi di mortalità dal 2021 (non rilevabile dal semplice confronto col valor medio).

Mi sembra opportuno concludere l’esempio facendo notare che proprio nella stessa regione dell’Uomo di Scienza che ne nega l’esistenza, l’eccesso di mortalità delle adolescenti raggiunge il 60%!  No comment….

Questi dati sono facilmente verificabili mediante le elaborazioni Istat accessibili dalla piattaforma Tableau Public (8). L’unica avvertenza è qui che non sono compensati sulla demografia.

Basta scegliere “dati mensili”, specificare la Regione, selezionare le classi d’età e il sesso,  quindi il confronto tra il 2023 e la media 2015-2019.

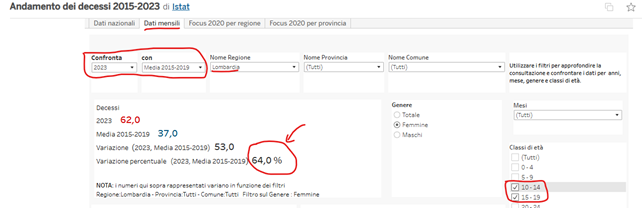
Fig. (..) Schermata del sito “Tableau Public” da cui si può verificare l’eccesso di mortalità delle ragazze in Lombardia nel 2023

https://public.tableau.com/app/profile/istat.istituto.nazionale.di.statistica/viz/Andamentodeidecessi2015-2023/Datinazionali

Risultati salienti dell’analisi di eccesso di mortalità 

Dopo questi esempi della qualità delle informazioni fornite dalla Scienza, vorrei passare ad illustrare i risultati ottenuti dallo studio da me realizzato secondo i criteri esposti in precedenza.

Con gli stessi principi generali, e per gli stessi 36 gruppi di popolazione, ho elaborato sia gli eccessi di mortalità annuali che quelli giornalieri.

Questo permette di aggiungere alla conoscenza del valore di eccesso di mortalità annuo, di per sé importante, anche la conoscenza dell’andamento temporale, mediante grafici molto simili a quelli realizzati dal sito Our World in Data (9)

https://ourworldindata.org/covid-deaths

Questa analisi dettagliata ha permesso di mettere in luce diversi aspetti normalmente assenti dalle analisi rese pubbliche.

Gli Istituti di sorveglianza sanitaria affermano che non si rileva eccesso di mortalità nella popolazione sotto i 50 anni, prendendo come riferimento la baseline della media 2015-2019.

Ebbene, l’analisi effettuata rende evidente che questa affermazione non corrisponde a verità.

Infatti, utilizzando lo stesso metodo di analisi, almeno tre gruppi sotto i 50 anni evidenziano eccessi dal 2021 in poi:

• I bambini 5-9 anni, sia maschi (2022, 2023) che femmine (2023);
• Le adolescenti 10-19 anni (2021, 2023)
• I giovani 30-39 anni e in misura minore 40-49 anni (2021).

Ovviamente i valori medi 2015-2019 sono sempre corretti per le variazioni demografiche, come da buona pratica.

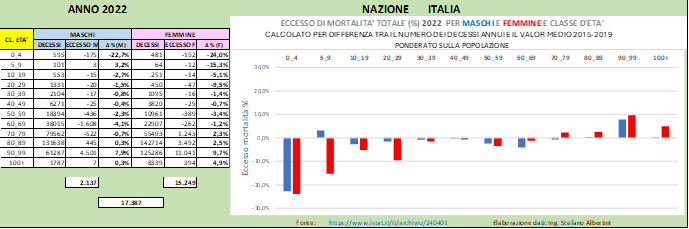
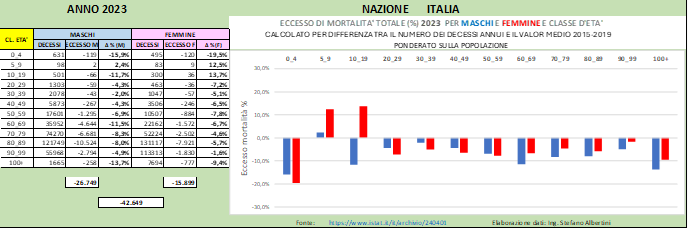
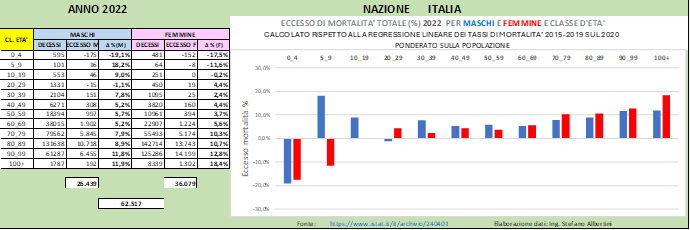
In Fig. (…) sono mostrati i valori di eccesso di mortalità annuali valutati rispetto alla media ponderata 2015-2019 e possiamo distinguere chiaramente gli eccessi elencati sopra.

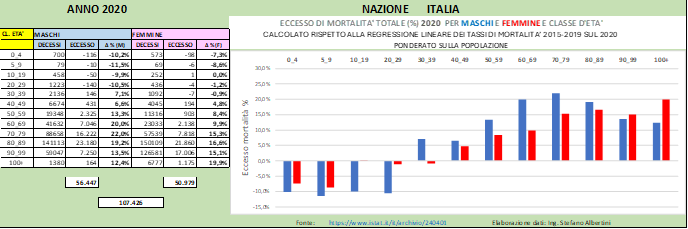
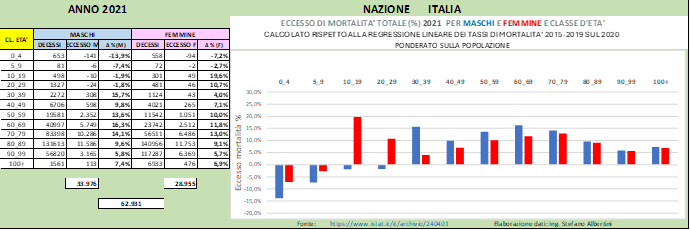
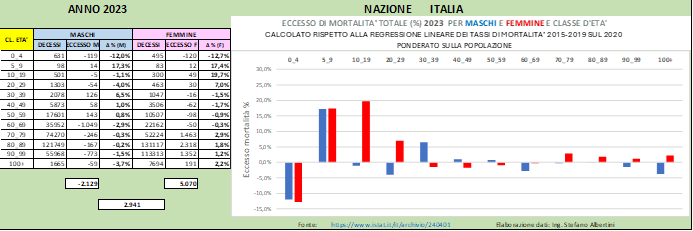
In Fig. (..) sono mostrate le stesse informazioni ma valutate tenendo conto della regressione lineare.

Si può notare che in generale tutti i gruppi di popolazione mostrano un eccesso di mortalità maggiore che nel caso precedente. Visti con questa prospettiva, gli eccessi di mortalità giovanili sono molto più evidenti

Il primo metodo, citato da I.S.S. e Istat nel documento (7), fornisce risultati che devono ritenersi cautelativi ed è largamente applicato nell’analisi delle popolazioni più giovanili.  Tuttavia, l’andamento dei tassi di mortalità regolare di alcuni gruppi di giovani, come ad es. i maschi 10-19 anni (Fig. ..) e i maschi 30-39 anni (Fig. ..) suggerisce che tra i due metodi la regressione lineare sia il più appropriatoi, il che getta ulteriori ombre sulla narrazione ufficiale.

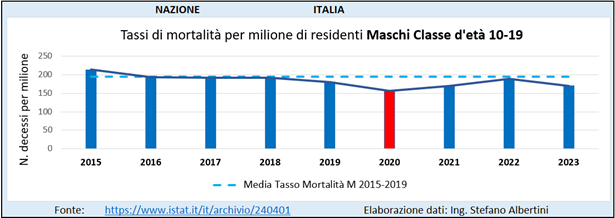
Per quanto riguarda i gruppi di popolazione sopra i 50 anni, non ci sono dubbi che sia il metodo di analisi più corretto.

Risulta evidente che in tutti i gruppi di età > 60 anni la mortalità si mantiene in eccesso nel 2021 e nel 2022, e in alcuni anche nel 2023. Si nota come la mortalità non accenni a decrescere come ci si aspetterebbe dopo una stagione pandemica così intensa (effetto harvesting), anzi nel 2022 si assiste ad una recrudescenza che peggiora con l’avanzare dell’età.

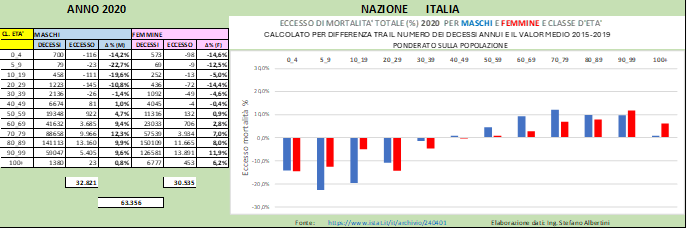
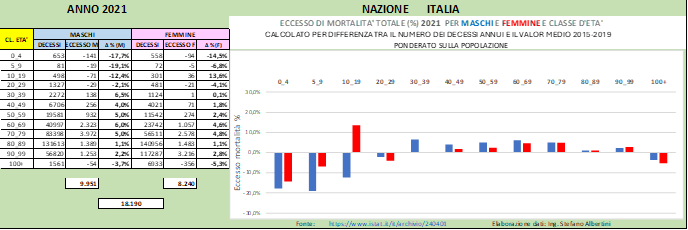
Un altro modo di descrivere l’eccesso di mortalità, oltre alla rassegna dei valori annuali per tutti i gruppi di popolazione, è sceglierne uno e osservare l’andamento dell’eccesso giornaliero per quattro anni.

Il metodo di calcolo si basa sugli stessi principi ma qui è applicato giornalmente.

Si possono vedere (Fig. (..) e seguenti) nei riquadri in basso corrispondenti ad ogni anno il numero di decessi attesi, l’eccesso numerico e la variazione percentuale rispetto all’atteso. La variazione percentuale indicata corrisponde alla variazione del valore della curva nell’anno solare. Il totale annuale può essere positivo anche se la curva assume per tutto l’anno valori negativi. 

Ad esempio: se al 31dicembre dell’anno precedente il valore parte da -30% e a fine anno corrente vale -10%, la variazione annuale è stata del +20%. I grafici di questo tipo si dicono cumulativi perché il dato di ogni giorno si somma al totale maturato al giorno precedente a partire dall’inizio del periodo di analisi (primo gennaio 2020).  Questo permette di seguire l’evoluzione della variabile (eccesso di mortalità): più che i valori assoluti sono importanti le variazioni.

I grafici giornalieri sono utilissimi per seguire con grande precisione temporale aumenti anomali della mortalità, inversioni di tendenza, ecc.: tutte informazioni che in presenza di aumenti inattesi di mortalità possono dare indicazioni preziose per individuare eventuali correlazioni con potenziali fattori scatenanti.

Dopo questa doverosa introduzione, dovrebbe essere più chiaro interpretare i grafici.

Nel seguito mostro i grafici giornalieri relativi all’eccesso di mortalità dei tre gruppi giovanili in cui rispetto alla media 2015-2019 si è manifestato un aumento di mortalità dopo il 2020, e di un gruppo di anziani, quest’ultimo valutato con regressione lineare.

Vediamo in Fig. (..) l’andamento nei bambini maschi. La particolarità che salta all’occhio è che la curva nettamente in discesa a un certo punto verso metà 2022 cambia decisamente tendenza e prosegue in salita sino a metà 2023, come se fosse rimbalzata.

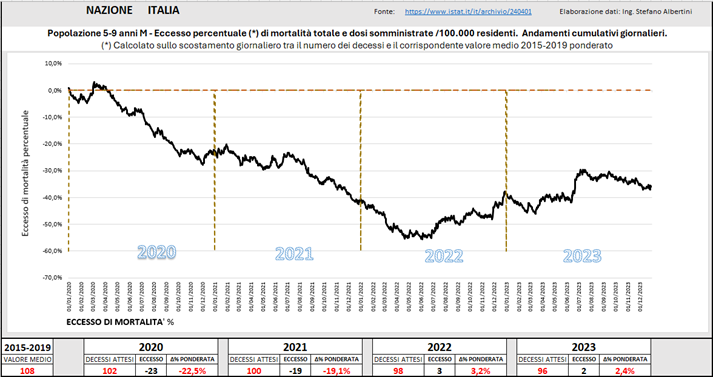
Fig. (..)

In Fig. (..) è rappresentato l’andamento dell’eccesso di mortalità dei giovani maschi 30-39 anni, sempre valutato nella modalità più cautelativa. In questo caso si osserva un aumento della mortalità iniziato a metà del 2021, che si mantiene per tutto l’anno, e con minore intensità nella primavera successiva. 

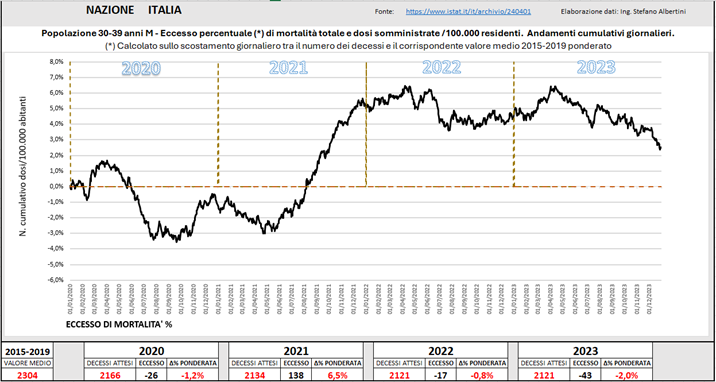
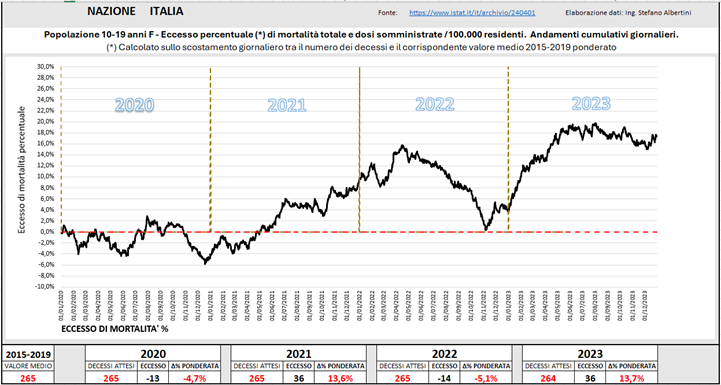
In Fig. (..) vediamo l’andamento dell’eccesso di mortalità delle adolescenti (10-19 anni), che il è gruppo di popolazione più colpito, e uno dei più colpiti in assoluto dall’eccesso di mortalità.

Il metodo utilizzato è sempre quello più cautelativo.

Questo andamento è più complesso degli altri, perché comporta aumenti e diminuzioni della mortalità ad anni alterni. Inoltre, l’ultima repentina salita della mortalità si manifesta con un’inversione di tendenza talmente netta che fa pensare a una precisa causa scatenante.

L’ultimo esempio che vorrei portare è relativo ad un gruppo di popolazione anziana, per la precisione la classe 80-89 anni senza distinzione di genere. In questo caso l’eccesso è stimato col metodo della regressione lineare per i motivi specificati in precedenza. Con i circa 250.000 decessi annui, questa classe d’età da sola rappresenta circa il 40% dei decessi nazionali, e sommando le classi limitrofe si raggiunge circa l’85%, pertanto l’andamento dei decessi è rappresentativo della totalità della popolazione. Come si può osservare dalla Fig. (..), questa curva di eccesso di mortalità riproduce nei minimi dettagli quella proposta dal sito Our World in Data, che è relativa all’intera popolazione ed è ottenuta analogamente con baseline costruita con regressione lineare dei dati 2015-2019. 

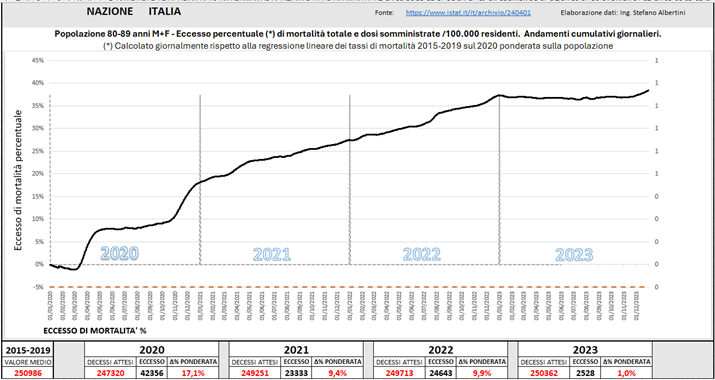
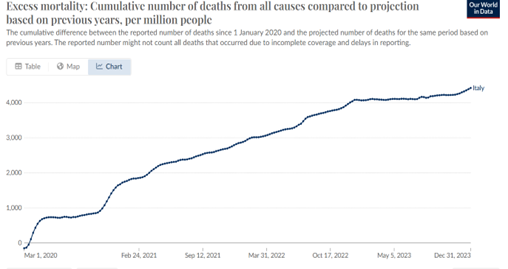
Fig. (..)

Tornando al contenuto del grafico si osserva che, dopo le due ondate pandemiche del 2020 sconfinate nel 2021, l’eccesso di mortalità continua a salire senza soluzione di continuità, senza quel rallentamento che dovrebbe essere fisiologico dopo la “mietitura” pandemica. In più, guardando attentamente si notano due gradini dopo la metà del 2022 e a fine 2022. Si osserva che questa strana conformazione si acuisce con l’avanzare dell’età della popolazione, inoltre per la cronaca si riscontra anche in altri paesi.

Le correlazioni con le vaccinazioni: teoria del complotto?

Una volta disponibili i grafici dell’eccesso di mortalità con dettaglio giornaliero, può essere utile sovrapporre gli andamenti di fattori esterni che possono aver influenza sulla salute, meglio se noti con pari dettaglio.

La Scienza spesso sovrappone le ondate di calore, ne è un esempio il già citato documento (7) dove anche con dati molto meno dettagliati riesce a stabilire addirittura una correlazione causale.

Io in realtà mi accontento di mostrare correlazioni temporali, dalle quali eventualmente altri ricercatori con competenze mediche potrebbero, perché no, prendere spunto per verificare l’esistenza di nessi causali.

Perché sovrapporre proprio le somministrazioni vaccinali? Intanto rappresentano un evento credo unico nella storia di somministrazione sistematica di farmaci non completamente testati, e si presume che questo abbia un effetto (a priori, positivo o negativo) sulla salute e sulla mortalità della quasi totalità della popolazione. Inoltre, i dati di somministrazione sono noti con lo stesso grado di dettaglio raggiunto coi grafici giornalieri, e quindi ben si prestano a un confronto puntuale.

Proprio perché non si ha la pretesa di provare nessi causali con metodi grafici, si omette di rappresentare tutte le possibili covariate.  Cionondimeno, alcune di esse sono state passate in esame.

Per quanto riguarda i giovani, le principali cause di morte sono di natura traumatica: soprattutto suicidi e incidenti stradali.

I suicidi non sono pervenuti: purtroppo al momento in cui si scrive i dati sono aggiornati al 2021 e comunque sono suddivisi in fasce d’età troppo larghe per poter essere utilizzati in questo studio.

Incidenti stradali: dopo la fermata per il lockdown, nella popolazione sopra i 15 anni si è avuto un aumento fino al 2022, quando i valori (compensati per la demografia) in tutte le classi d’età sfiorano la media 2015-2019, poi nuova flessione nel 2023.  Per la popolazione da 5 a 14 anni gli andamenti sono più casuali e si possono avere modesti eccessi rispetto alla media, spesso compensati da difetti in altri anni. In conclusione, gli incidenti stradali non giustificano particolari eccessi di mortalità.

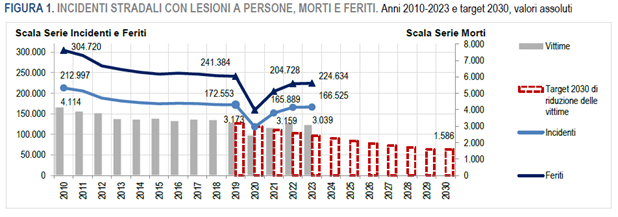
Fig. (..) Andamento generale degli incidenti stradali e relativi decessi fino a tutto il 2023 (da Rapporto Istat)

Decessi per Covid-19: fatto salvo l’altissimo margine di aleatorietà con cui vengono conteggiati i decessi per questa causa, pare comunque un paradosso considerare tali decessi una covariata nell’analisi di possibili effetti collaterali di un farmaco che avrebbe dovuto evitarli.

Con queste doverose premesse, vado a mostrare qualche esempio di grafico combinato eccesso di mortalità + somministrazioni, partendo proprio dagli stessi grafici mostrati in precedenza.

BAMBINI 5-9 ANNI

Nella figura sottostante si possono osservare i due grafici sovrapposti. Si tratta della popolazione maschile di età 5-9 anni.  La linea blu rappresenta il cumulativo delle dosi somministrate (prime, seconde e in misura minore terze).

Giova ribadire che questi grafici sono cumulativi, pertanto sono significative le variazioni piuttosto che i valori assoluti.  In altre parole, nel caso specifico si può vedere che a giugno 2022 la curva ha raggiunto un valore intorno a – 55% (variazione rispetto al 1° gennaio 2020) in virtù di un andamento fortemente in calo della mortalità rispetto alla media 2015-2019. A partire da quel momento, la tendenza si è capovolta e la mortalità ha iniziato a crescere, arrivando dopo circa un anno a -30%. Nel periodo giugno 22 – giugno 23 la variazione è stata quindi di +25%, per poi scendere leggermente segnando una variazione annua piccola ma positiva nei due anni solari.

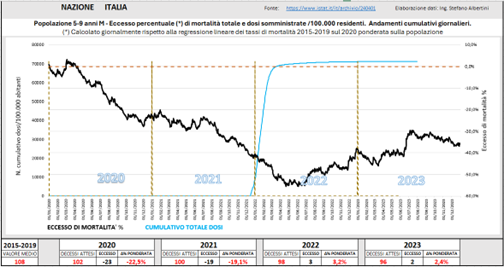
Fig. (..)

L’eccesso di mortalità nei bambini (di entrambi i sessi) si è riscontrato, oltre che nei dati nazionali, in numerose regioni. In particolare, è stato molto evidente in Emilia-Romagna (M+F), Toscana (M), Puglia (M+F), Umbria (F), Marche (F). Inoltre, si è avuto un aumento apprezzabile in Toscana(F), Abruzzo (F), Campania (F), Piemonte (M), Veneto (M), Marche (M).

Si mostrano nel seguito due delle situazioni regionali di particolare rilievo: Toscana ed Emilia-Romagna.

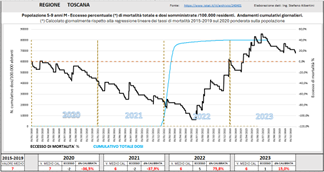
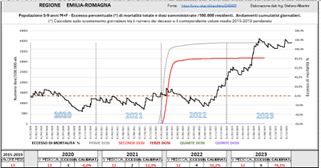
Fig. (..)

GIOVANI MASCHI 30-39 ANNI

La figura sotto mostra la combinazione dell’eccesso di mortalità dei trentenni con le relative somministrazioni.  L’eccesso di mortalità di questa classe di popolazione è stato piuttosto diffuso su buona parte del territorio nazionale, in particolare in Toscana, Umbria, Lazio, Veneto, Friuli-VG, Campania, Basilicata, Puglia, Sicilia, Sardegna.

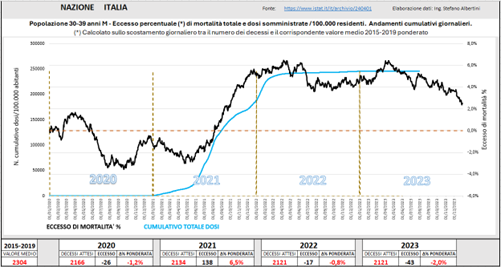
Fig. (..)

Nel seguito si mostrano alcuni esempi a livello regionale, ove tale fenomeno si è manifestato in maniera molto più pronunciata che a livello nazionale. Tali esempi non sono esaustivi di tutta la casistica riscontrata ma giocoforza si è operata una selezione.

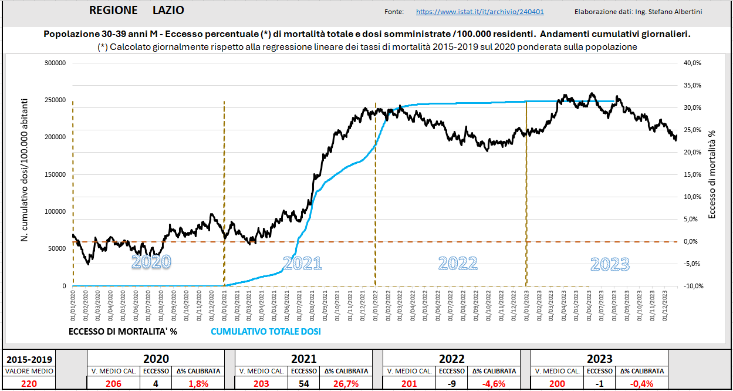
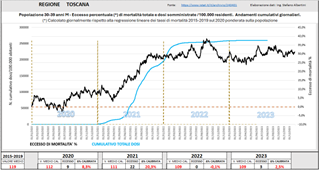
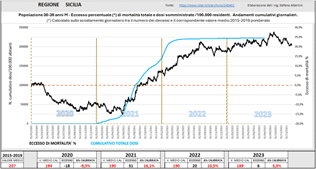
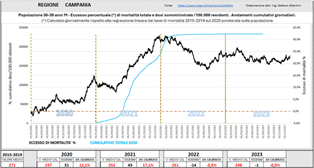
Fig. (..)

RAGAZZE 10-19 ANNI

Questo gruppo di popolazione merita un’attenzione particolare perché come sottolineato in precedenza è la classe giovanile che è stata maggiormente colpita dall’eccesso di mortalità, e nella quale quest’ultimo si è manifestato in due fasi distinte.

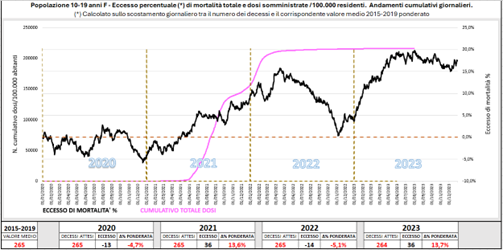
Fig. (..)

Nella figura si nota che il primo aumento di mortalità si accompagna alla fase di salita della curva delle somministrazioni, più o meno come avviene per i trentenni maschi. Dopo la fase di discesa, il secondo aumento di mortalità, molto più deciso, sembra non trovare corrispondenza con una particolare fase di somministrazioni.

Questo finché non si isolano dalle altre le somministrazioni delle quarte dosi.

Se si inserisce nel grafico la sola curva delle quarte dosi (con numeri decisamente più piccoli), si trova una corrispondenza sorprendente con la seconda fase di salita della mortalità.

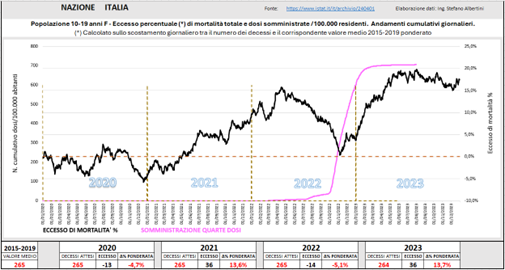
Fig. (..)

Si trova quindi una doppia correlazione temporale tra eccesso di mortalità e somministrazioni.

Quando ho fatto questa “scoperta”, mi è sembrata una cosa enorme e ho voluto guardare le cose anche da un altro punto di vista. Ho pertanto fatto ricorso a un altro tipo di grafico giornaliero, non più cumulativo ma che mostra i valori così come sono, senza sommarli. È semplicemente “filtrato” per eliminare le eccessive oscillazioni.  Per gli amanti della matematica, i valori di questo grafico corrispondono alla pendenza (in positivo o negativo) di quello cumulativo.

Le dosi rappresentate sono solo le quarte. Nella figura sotto si vede ancora più nettamente una situazione molto particolare, dove a sette mesi continuativi di mortalità in fortissimo calo ne sono seguiti altrettanti in continuativo e fortissimo eccesso, con le quarte dosi a fare da spartiacque.

A guardare bene, si intravede anche un’analogia di forma tra la curva delle somministrazioni e quella dell’eccesso di mortalità, con un certo sfasamento temporale che qui è stato stimato in 38 giorni.

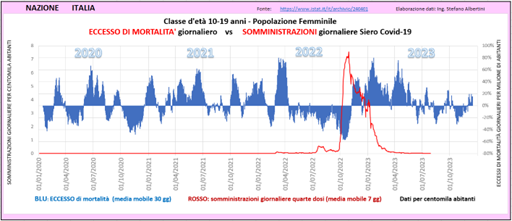
Fig. (..)

Queste correlazioni temporali così sorprendenti mi hanno portato a effettuare analisi più approfondite, partendo da questo gruppo di popolazione ma anche estendendolo in ambito regionale per la stessa fascia d’età e genere. Quello che sta emergendo è che traslando in avanti sull’asse dei tempi le curve delle somministrazioni si ottiene una forte corrispondenza a livello numerico (e quindi di forma) tra i due grafici. In questo gruppo di popolazione, in particolare, questo si ripete per tutte le dosi somministrate. Questo studio è ancora in corso, per cui preferisco non entrare troppo nei dettagli

Nella figura sotto si possono vedere i tratti della curva in cui è possibile riconoscere correlazioni temporali oggettive tra le cure delle somministrazioni e quelle dell’eccesso di mortalità.

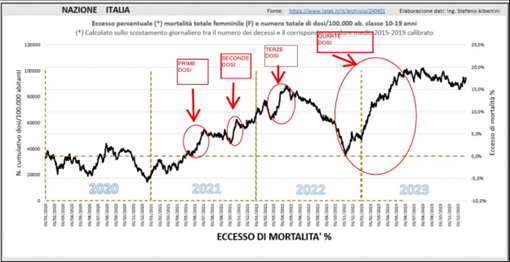
Fig. (..)

Questo particolarissimo andamento combinato dell’eccesso di mortalità e delle somministrazioni, per le giovani ragazze, si riscontra in maniera evidente anche a livello regionale.  Il caso numericamente più eclatante, citato in precedenza, è quello della Lombardia. La Campania invece offre un esempio notevole per la rapidità di salita del secondo picco di mortalità.

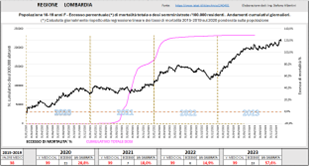
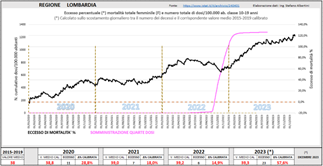
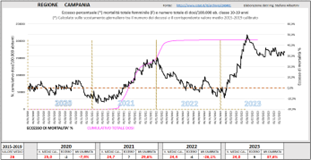
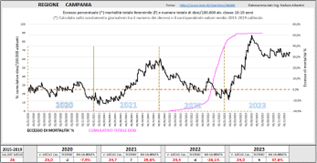
Fig. (..)

ANZIANI 80-89 ANNI

Anche l’andamento dell’eccesso di mortalità degli anziani riserva aspetti interessanti.

Oltre all’assenza di flessione nella crescita di mortalità, già di per sé un’anomalia, si notano due gradini che nel 2022 portano ad un ulteriore incremento della mortalità. Questi gradini, in particolare il primo (luglio 2022) sono stati catalogati come una conseguenza delle ondate di calore. Notiamo però che in qualche modo ripropongono l’andamento delle quarte dosi.

Questa peculiarità si apprezza anche nella figura sottostante, che riporta gli andamenti giornalieri non cumulati.   

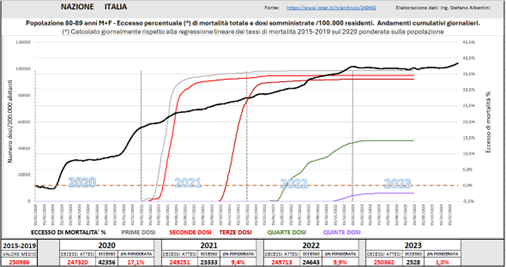
Fig. (..)

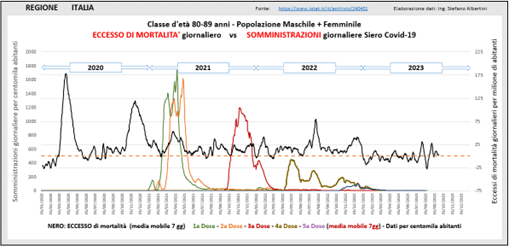
Fig. (..)

ITALIA DEL CENTRO E DEL SUD: L’ALTRA PANDEMIA

Come molti sanno, a livello di dati annuali gli eccessi di mortalità si sono prodotti in maniera molto diversa nelle Regioni del Nord (e in Italia), in quelle del Centro e in quelle del Sud.

Nella figura sotto si portano ad esempio i dati della Lombardia in rappresentanza del Nord, della Sardegna in rappresentanza del Centro e della Campania in rappresentanza del Sud (eccessi di mortalità in dati assoluti).

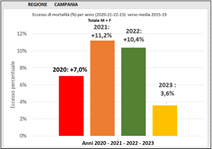
Fig. (..)

E’ interessante vedere come tutto ciò si traduce in grafici giornalieri, mettendo a confronto la stessa classe d’età: anziani 80-89 anni entrambi i generi.

Come si può vedere dalle figure seguenti, la Lombardia ha registrato numerosissimi decessi nella prima parte del 2020, durante la prima ondata pandemica; in misura inferiore nella seconda ondata di fine anno. Nonostante un eccesso prossimo al 40% nel 2020, stranamente la mortalità ha continuato a crescere negli anni successivi, in particolare nel 2022 quando gli strani “gradini” portano il conteggio dell’eccesso di mortalità a sfiorare il 10%.

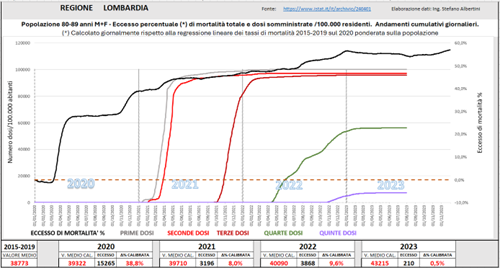
Fig. (..)

In Sardegna la prima ondata del 2020 è praticamente assente, mentre si presenta la seconda quella di fine anno. Dal grafico però si nota che l’anno peggiore è il 2022, con tre dosi di vaccinazione già effettuate e la quarta in pieno svolgimento.

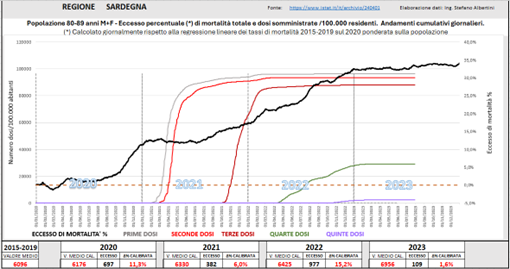
Fig. (..)

In Campania, il picco pandemico è ancora più modesto, e tra l’altro accenna a diminuire quando qualcosa scatena una fase ben più importante di eccesso di mortalità che perdura regolarmente per due anni di seguito per flettere (neanche del tutto solo nel 2023.

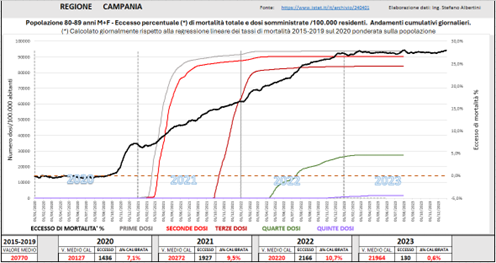
Fig. (..)